Time for an uncharacteristically political post. This will also likely be the first in a series of posts. I will link the rest of them here at the start as I finish them.
To see the rest of the posts in this series, click the "cybernetics" tag in the box on the right. Two paragraphs up if using a text-mode browser.
The case for planning
The last few years the climate situation and market economies' inability to address it has caused me to read up on political theory to try and figure out what can be done. I haven't written much about this journey on here, but those who know me know that this process has been going on for quite a while. My conclusion so far is that the old Soviet cyberneticians were on the right track.
This all ties to what is known as the economic calculation problem (ECP). The debate revolves around whether planning is feasible as a replacement for markets. This debate raged primarily in the interwar years and is one which never had a satisfactory conclusion. Since the dissolution of the USSR between 1989-1991 the debate seemed to have been settled in favor of markets. After the end of the USSR the idea of free market capitalism as the final stage of humankind emerged, what we today know as neoliberalism, the dominant global ideology.
Today neoliberalism faces the challenge of how to address the ongoing climate catastrophe in a way that does not place undue burden on the unelected elite that owns the economy. This gives rise to policies that create tension between the different sections of the working classes. One recent example of this is the yellow vest movement, triggered by the Macron government's fuel taxes.
One reason for the rise of movements like the yellow vests is the idea that greenhouse gas (GHG) emissions must have a cost. And as we all know, whatever has a fixed cost is effectively free if you're rich, and taxes on consumption like VAT are regressive in practice. Another complication is that people living in cities are less affected by fuel taxes than people living in rural areas, especially up here in northern Sweden where distances are far and most social services have moved to the cities.
The fair and rational solution to the climate situation, which the market system has proven itself unable to deal with, is a global planned economy. I will not concern myself too much with the politics behind the plan in these posts, other than to say that I prefer if the political process is as democratic as possible. It should also be pointed out that the workplaces that most of us spend half our waking time in is by no means democratic. In most private companies all decisions are taken by the company's owners, which are never elected or drawn by lot or any such process. In addition, no company uses a market system internally. Neither do families.
Beyond being more democratic, planning also has the potential to be much more efficient than markets, meaning the same standard of living can be maintained with less labour input. This will be important as humanity transitions from capitalism into a sustainable steady-state economy.
Why the economic calculation problem is easier than previously thought
Back in the 1920's up to the 1940's when the ECP debate raged the counterargument to economic planning from people like Friedrich Hayek was that there is simply no practical way to rationally allocate resources in-natura for an entire economy. If you have say 1000 goods then it would take 10003 = one billion operations to solve the related linear equations. So the argument went that a team of humans working with calculators could not hope the finish the calculations within the span of a human lifetime, even for quite modest economies.
To the modern reader there is perhaps an obvious solution to this problem: computers. In the time the ECP debate raged, the term computer was a job title, like professor or plumber. It would take until some time after the second world war for computer science to be properly established. Modern computers can perform billions of calculations per second, cheaply.
What kind of computations do we need?
Having realized that computers can plan economic activity, the question become "how much of it?". The answer turns out to be "quite a lot"!
Wassily Leontief developed the concept of input-output analysis around 1936. This involves finding the solution to a linear equation system on the form (I - A)x = d where A is a matrix of technical coefficients saying how much of each good is required to produce one unit of some other good, d is a given vector of final demands and x is a vector saying how much of each good to produce, including intermediate goods. Solving such a system naïvely using Gaussian elimination indeed takes time cubic in the number of variables. But as even Leontief noted, the matrix A has many entries that are zero. A is sparse.
Dealing with sparse matrices is at present a scientific field unto itself. Modern computers routinely solve sparse linear system in tens of millions of variables, and computer clusters can deal with billions of variables. So far so good.
What's the catch?
Solving linear systems is unfortunately not enough. In reality there are limitations to how much each industry can produce, how many people can work in each industry, transport limitations, how much GHG may be emitted and so on. Solving constrained linear systems like this is known as linear programming. LP is a much more difficult problem than just solving a linear equation. So much more difficult that finding an optimal solution is suspected to take time exponential in the number of variables, not cubic. Not good!
How do we solve LP in reasonable time then?
The key to using LP for economic planning is realizing that we don't need an optimal solution. An approximate solution works just as well, provided it's known to be close enough to the optimum, say within 1%. There is a whole class of algorithms that can do this. The following table is a summary with simplified big-O notation:
| Who | When | Complexity | Worst case |
|---|---|---|---|
| Khachiyan | 1979 | O(n6L) | O(n6L) |
| Karmarkar | 1984 | O(n3.5L) | O(n3.5L) |
| Renegar | 1988 | O(d2.373n0.5L) | O(n2.873L) |
| Vaidya | 1989 | O((n+d)1.5nL) | O(n2.5L) |
| Lee and Sidford | 2015 | O((nnz(A) + n2)n0.5L) | O(n2.5L) |
| Cohen, Lee and Song | 2020 | O(n2.373L) | O(n2.373L) |
nnz(A) is the number of non-zero elements in A, d is the number of variables, n is the number of constraints, d < n. L is the desired accuracy of the solution, in bits.
In practice many of these algorithms are slower since matrix multiplication is O(n2.8) for n that modern computers can actually handle. For a real economy n will be on the order of 109, which still makes the computations impractical if run on a single computer. There is a need to evaluate how well LP can be solved on computer clusters, especially as the number of nodes N approaches √n, n or even nnz(A). The notion here is that every workplace could have a computer that participates in the planning process, or perhaps a computer cluster per city, all connected over the internet. The more nodes that are connected together, the more efficient the economy becomes.
In a future post I will go into detail on my findings what algorithms seem suitable for parallelization, and some experimental results.
Other considerations
The ideas in this section are mostly taken from this paper from 2020 by Spyridon Samothrakis.
Real economies are not linear. There are synergies, overhead, depreciation and diminishing returns. The following plot illustrates how the requirements for a section of the chemical industry might depend on how much of its output is called for:
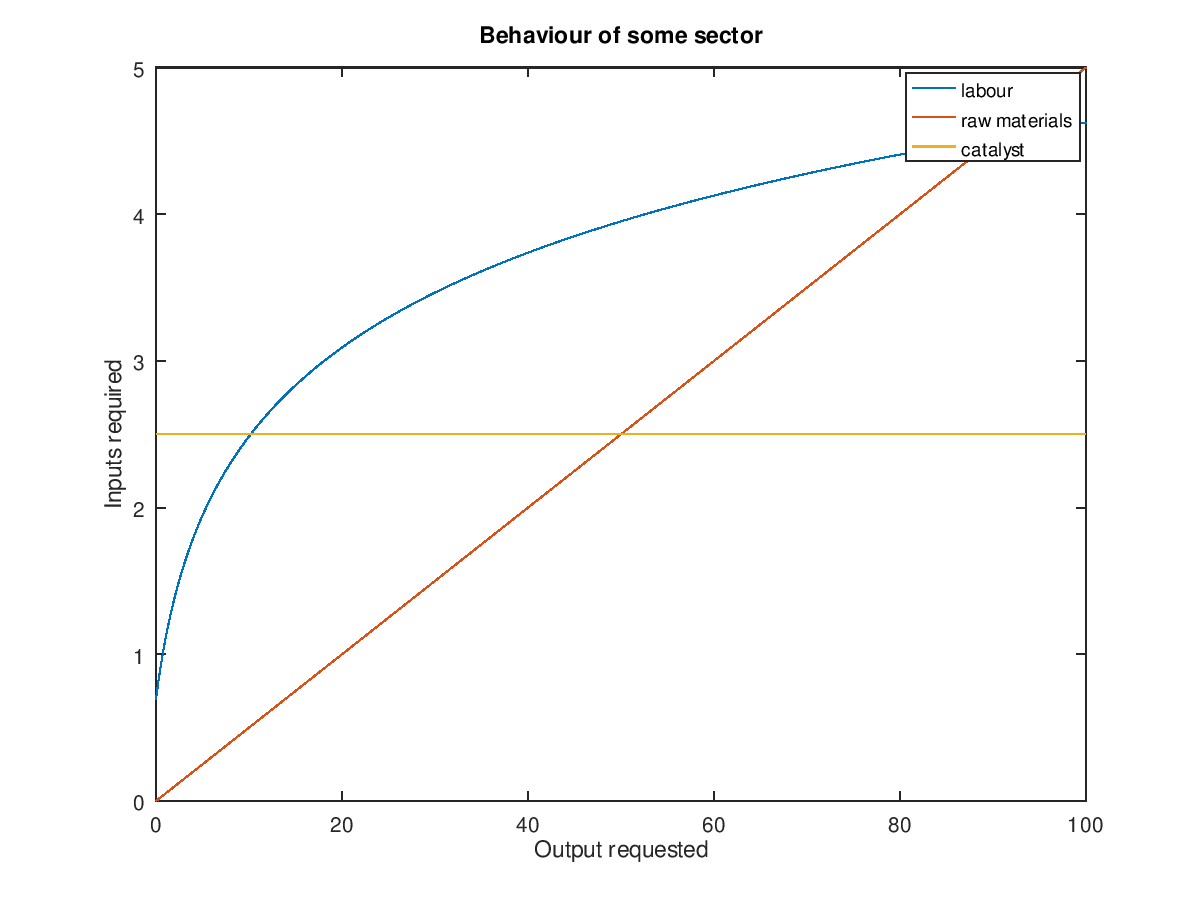
The line for raw materials demonstrates the kind of linear model that Leontief assumes. The labour curve demonstrates how larger-scale production might reduce the marginal labour requirements in some sector, and that small-scale production often results in mediocre output. The labour curve is also non-zero for no output, which models how some industries will have overhead inherent from just sitting around. Finally the catalyst curve is for demonstrating that there may be inputs that change very little regardless of demand.
This sort of non-linear behavior may be wildly different between sectors. In principle it can be captured by piecewise linearization. Another option is to move toward either quadratic programming (QP) or general mathematical programming.
Further reading
For an overview of how a society based around computerized planning might work, I recommend reading Towards a New Socialism by Paul Cockshott and Allin Cottrell.
Other related reads:
- The People's Republic of Walmart by Leigh Phillips and Michal Rozworski
- The Cybernetic Brain by Andrew Pickering
- Brain of the Firm by Stafford Beer
Some names of people in this field in no particular order:
For those who prefer podcasts I can recommend General Intellect Unit which should be available wherever you get your podcasts.